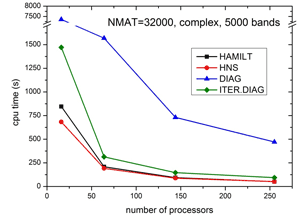
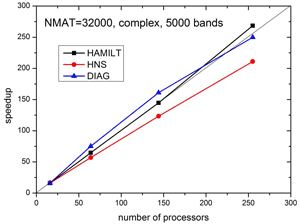
Specifically, we use the WIEN2k program package [1], which was developed over the last 30 years in our group. It is licensed worldwide by more than 1700 groups at universities and in industries and is one of the most accurate and most used packages for electronic structure simulations of solids. It is written in FORTRAN 90 and the individual modules are linked together via C-shell scripts. The main computational task is the setup and diagonalization of a generalized eigenvalue problem. The resulting matrices can have sizes of up to 100000x100000, which requires a memory of at least 200 GB. The program runs highly parallel using mpi, Blacs and Scalapack libraries. Diagonalization, which usually is the bottleneck of such calculations has been changed to a recently developed [2] iterative scheme which is up to 10 times faster than conventional methods. As illustrated in Fig. 1, this reduces the diagonalization time to the same order of magnitude as setting up the problem. Both, setup and diagonalization scale very well up to 512 processors, which has been achieved due to careful (nearly 100%) parallelization without any communication of the setup, but also Scalapack routines scale very well due to the fast network of the VSC.
Two specific applications will be described below:
Supported Au nano-particles are considered as promising oxidation catalysts with superior low temperature activity and selectivity in a variety of chemical reactions. However, supported nano Au-catalysts are facing a major problem with sintering under typical reaction conditions. For the case of the Au/TiO2(110) system oxygen vacancies or oxidized (alkaline) TiO2(110) may provide nucleation sites for immobilizing the Au clusters up to 500K. However, the microscopic processes that are responsible for the low temperature activity of Au particles on TiO2(110) are still controversially discussed in literature. The recently discovered nanomesh of hexagonal BN (h-BN) on Rh(111) and on Ru(0001) offers a unique sturdy oxygen-free template for supporting Au nanoparticles. The h-BN/Rh(111) nanomesh consists of a periodic hexagonal array of 2 nm wide pores with a lattice constant of 3.25 nm. It can be modeled by a 12x12 supercell of Rh(111) and a 13x13 supercell of h-BN on top of the 3 layer metal slab (Fig. 2). Due to the lattice mismatch and the interaction with the metal substrate the h-BN layer is not flat, but forms a warped structure with holes and rims [3].
 |
 |
 |
 |
The h-BN nanomesh can be viewed as a highly regular network of trapping sites (holes) in which deposited Au atoms preferentially condense into Au nano particles. This allows the preparation of well-ordered model catalysts. Calculations of preferred adsorption sites of these Au particles and their properties are under way. It should be mentioned that due to the large size of these unit cells such calculations can only be performed on very powerful parallel computers like the VSC.
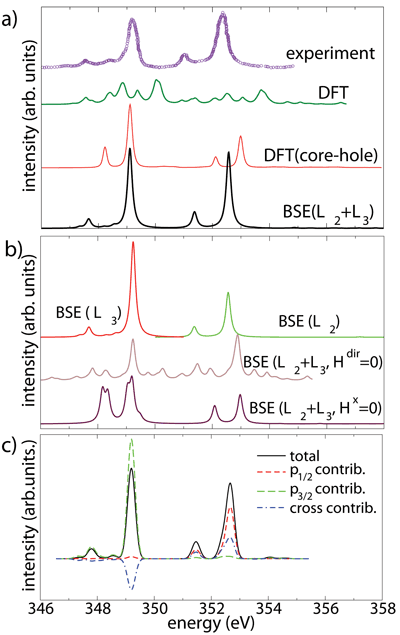
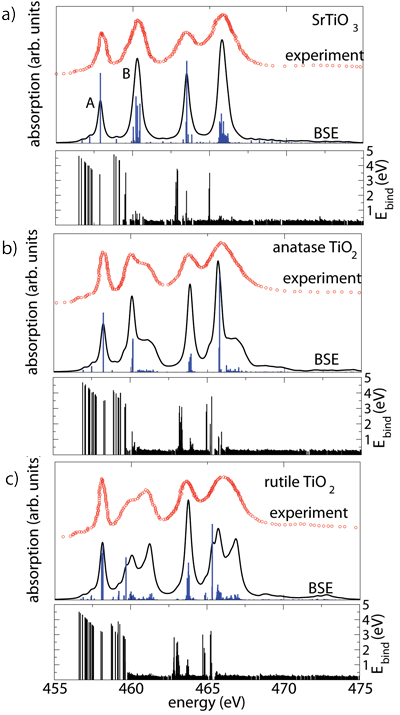
Another problem concerns the L2,3 X-ray absorption (XANES) spectra of early transition metal compounds. When a core electron from the 2p shell is excited into empty conduction bands, the resulting hole and the excited electron interact with each other and a single particle description breaks down. These excitonic effects require the description by a 2-particle (electron-hole) approach and can be treated within the Bethe-Salpeter equation (BSE). Solving the BSE requires again the setup and diagonalization of large matrices and the VSC is ideally suited for this due to the large available memory and the fast interconnect of the cluster nodes. Fig. 3 shows the results of such a calculation for the Ca L2,3 edge in CaF2 together with the experimental spectra as well as the calculations using single particle DFT approaches. Only the BSE approach can reproduce and explain the experimental spectrum, both in terms of intensities as well as the observed energy splitting. Furthermore we can identify the effects of Coulomb and exchange between the hole and the electron as well as the individual contributions of the spin-orbit splitted p1/2 and p3/2 contributions. The observed intensities, which differ significantly from the simple 2:1 ratio of a single particle picture, are due to coherent cross terms in the squared momentum matrix elements of the p1/2 and p3/2 states. Another example is shown in Fig. 4 for the Ti L2,3 spectra of three different Ti oxides, where the very small differences in the experimental spectra could be very well explained in the calculations. The observed L3/L2 intensities are again due to the coherent superposition of 2p1/2 and 2p3/2 contributions, but also the commonly assumed origin of the splitting within one sub-spectrum (either L3 or L2) is not simply due to the crystal field splitting of the 3d-eg and t2g electrons, but their shape and intensities are significantly modified by excitonic effects and cross terms.
Further information can be found at www.imc.tuwien.ac.at/staff/tc_group_e.php and vicom.univie.ac.at.
 |
 |
[1] Software package WIEN2k (P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, 2001). www.wien2k.at
[2] P. Blaha, H. Hofstätter, O. Koch, R. Laskowski, K. Schwarz: Iterative diagonalization in augmented plane wave based methods in electronic structure calculations; Journal of Computational Physics, 229 (2010), 453-460. http://publik.tuwien.ac.at/files/PubDat_178426.pdf
[3] R. Laskowski, P. Blaha: Ab initio study of h-BN nanomeshes on Ru(001), Rh(111), and Pt(111); Physical Review B, 81 (2010), 075418. http://publik.tuwien.ac.at/files/PubDat_184756.pdf
[4] R. Laskowski, P. Blaha: Understanding the L2,3 x-ray absorption spectra of early 3d transition elements; Physical Review B, 82 (2010), 205105. http://publik.tuwien.ac.at/files/PubDat_188807.pdf
