Wie schnell sind schnelle Fourier-Transformationen ?

Herbert Karner
karner@titania.tuwien.ac.at

Christoph W. Überhuber
christof@uranus.tuwien.ac.at

Institut für Angewandte und Numerische Mathematik, Technische Universität Wien

Die Erfindung immer leistungsfähigerer Algorithmen hat die Problemlösungskapazität moderner Computersysteme mindestens genauso stark vorangetrieben wie die Fortschritte der Computertechnologie in den letzten Jahrzehnten. Ein Meilenstein war die Erfindung der "schnellen Fourier-Transformation" (FFT). Dieser Algorithmus wurde in Dutzenden Programmen in höchst unterschiedlicher Qualität implementiert. Die Geschwindigkeit der verschiedenen FFT-Programme kann - je nach Problemgröße und Computertyp - um mehr als das Zehnfache divergieren. Im folgenden Beitrag wird der Frage nachgegangen, welche Softwareprodukte sich für wirklich schnelle Fourier-Transformationen eignen.

Diskrete Fourier-Transformationen (DFTs) finden vielfältige Anwendungen im Bereich der Natur- und Ingenieurwissenschaften, sei es bei der Filterung gestörter Signale oder im Rahmen der numerischen Lösung von partiellen Differentialgleichungen. Andere - "alltägliche" - Anwendungen der DFT findet man z. B. in Computertomographen oder bei der Kompression von Audio- und Video-Daten (MP3 bzw. MPEG) zur Übermittlung im Internet.

Kern der DFT ist eine spezielle Matrix-Vektor-Multiplikation. Für einen Datenvektor der Länge N erfordert eine solche Berechnung der DFT - größenordnungsmäßig - N ² (komplexe) Additionen und Multiplikationen. 1965 publizierten Cooley und Tukey [3] einen Algorithmus, die "schnelle Fourier-Transformation" (engl. fast Fourier transform - FFT), der die Berechnungskomplexität der DFT von O (N ²) auf O (N log N) reduziert.

Durch diese drastische Reduktion der arithmetischen Berechnungskomplexität nahm die Bedeutung von DFT-Methoden enorm zu. FFT-Routinen sind zu einem wichtigen Bestandteil aller wissenschaftlichen Programmbibliotheken, wie z.B. IMSL, NAG und ESSL, geworden. Darüber hinaus gibt es eine Vielzahl von frei erhältlichen - public domain - FFT-Paketen und Routinen, die über das Internet verfügbar sind.

Dieser Beitrag widmet sich dem Leistungspotential von frei verfügbaren FFT-Programmen und einigen weit verbreiteten FFT-Programmen, die in kommerziellen wissenschaftlichen Programmbibliotheken enthalten sind.

Im Rahmen eines FWF-Spezialforschungsbereichs (SFB 011 "AURORA"), der sich mit Themen des Hochleistungsrechnens beschäftigt, wurde eine umfangreiche Vergleichsuntersuchung an 24 FFT-Programmen auf 6 Computersystemen (siehe Tabelle 2) durchgeführt (Auer et al. [2]). Dabei standen zwei Fragen im Mittelpunkt:

• Welche FFT-Programme erbringen die besten Leistungen (Laufzeit und Gleitpunktleistung),  d. h., wie ist der State-of-the-art (Stand der Technik) bei FFT-Algorithmen und Programmen ?
• Welche Computersysteme (an UNI und TU Wien) eignen sich besonders gut für FFT-Berechnungen und warum, d. h., welche Beziehungen bestehen zwischen bestimmten Eigenschaften der Hardware und der Leistung von FFT-Programmen ?
  

Die schnellsten FFT-Programme

Die folgenden fünf FFT-Programme erzielten die besten Laufzeiten:

FFTPACK von Paul Swarztrauber (National center for Atmospheric Research, Boulder, colorado) kann als "Klassiker" unter den FFT-Programmpaketen betrachtet werden. Die erste Version des in Fortran 77 geschriebenen  Pakets wurde bereits 1973 veröffentlicht. FFTPACK-Routinen dienten als Basis für die in der IMSL-Bibliothek enthaltenen FFT-Programme. FFTPACK Version 4.1 (Nov. 1988) ist über NETLIB (http://www.netlib.org/fftpack/index.html) erhältlich.

FFTW ("Fastest Fourier Transform in the West") von Matteo Frigo und Stephen Johnson (MIT Laboratory for Computer Science) ist das zur Zeit "innovativste" FFT-Programmpaket. In FFTW sind erste Ansätze zu einer architekturadaptiven FFT-Berechnung realisiert. In einer - zeitaufwendigen - Initialisierungsphase wird ein "Berechnungsplan" ermittelt, der die FFT-Algorithmen an die Speicherhierarchie des Rechners anpasst. Das in ANSI C geschriebene Programmpaket ist über http://theory.lcs.mit.edu/~fftw/ erhältlich.

Green: Sammlung von in C geschriebenen FFT Programmen von J. Green (Naval Undersea Warfare center, New London, CT). Die Programme sind über http://hyperachive.lcs.mit.edu/HyperArchive/Archive/dev/src/ffts-for-risc-2-c.hqx
erhältlich.

Ooura: Sammlung von in C geschriebenen FFT-Programmen von T. Ooura (Research Institute for Mathematical Sciences, Kyoto University). Die Programme sind über http://momonga.t.u-tokyo.ac.jp/~ooura/fft.html erhältlich.

Sorensen: Sammlung von in Fortran 77 geschriebenen FFT-Programmen von H. V. Sorensen (University of Pennsylvania). Das Programm ist über http://www.jjj.de/fxt/sorensen.tgz erhältlich.

Kommerzielle FFT-Programme

Zusätzlich zu den fünf besten, frei verfügbaren FFT-Programmen werden in diesem Beitrag auch die am häufigsten benutzten kommerziellen FFT-Programme einer Bewertung unterzogen.

IMSL Fortran 77 Bibliothek: Detaillierte Informationen zu den IMSL-Programmbibliotheken der Visual Numerics Inc. sind über http://www.vni.com/products/imsl/ erhältlich.

NAG Fortran 77 Bibliothek: Detaillierte Informationen zu den numerischen Programmbibliotheken der NAG Ltd. sind über http://www.nag.co.uk/ erhältlich.

"Numerical Recipes" Software: Die in der Buchreihe Numerical Recipes - The Art of Scientific Programming (Press et al. [6]) in den Programmiersprachen Fortran 90, Fortran 77, Pascal, C und BASIC veröffentlichten FFT-Programme sind über den Buchhandel oder über  http://www.nr.com/com/storefront.html zu erwerben.

Tabelle 1 gibt eine Übersicht über die wichtigsten Merkmale der untersuchten FFT-Software. Dabei zeichnen sich die frei verfügbaren FFT-Programme durch die (teils wesentlich) bessere Leistung und die kommerziellen FFT-Programme durch die (meist) größere Funktionalität aus.

Tabelle 1: FFT-Software, die in diesem Beitrag behandelt wird.

Leistungsbeurteilung

Für den Benutzer eines Computersystems, der auf die Lösung einer konkreten Aufgabenstellung wartet, ist vor allem die dafür erforderliche Zeit von Interesse, die von zwei Einflussgrößen - Arbeit und Leistung - abhängt:

.

Für den Anwender sind daher folgende Kenngrößen von Interesse:

1.    Die zu verrichtende Arbeitsmenge, die sowohl von der Art und Komplexität der Problemstellung als auch von Eigenschaften des Lösungsalgorithmus abhängt. Die Arbeitsmenge und damit der Zeitbedarf für die Problemlösung kann durch algorithmische Verbesserungen reduziert werden. So reduzieren z. B. FFT-Algorithmen die erforderliche Arbeitsmenge für eine diskrete Fourier-Transformation (eines Datenvektors der Länge N) von 2N ² auf ungefähr 5N log N arithmetische Operationen.

3.    Der Wirkungsgrad ist der Prozentsatz der Maximalleistung, der bei der Ausführung einer bestimmten Arbeitsmenge erreicht wird. Er bringt zum Ausdruck, in welchem Ausmaß die potentiellen Möglichkeiten des Computersystems von einem Programm genutzt werden. Er ist also eine Maßzahl dafür, wie gut die Implementierung, also die Umsetzung des Algorithmus in ein Computerprogramm, gelungen ist. Eine Erhöhung des Wirkungsgrades lässt sich durch Optimieren der Programme herbeiführen (siehe Überhuber [7]).

Die Rechenzeit der verschiedenen FFT-Programme kann - je nach Problemgröße und Computertyp - um mehr als das Zehnfache divergieren. Diese extremen Rechenzeitunterschiede sind größtenteils auf Implementierungs- und damit auf Wirkungsgradunterschiede zurückzuführen.

Maximale Gleitpunktleistung: Eine wichtige Hardware-Kennzahl ist die Maximalleistung (peak performance) P_max eines Computers. Sie entspricht der theoretisch möglichen Maximalanzahl von Gleitpunkt-Operationen, die von diesem Computer pro Zeiteinheit durchgeführt werden können. Falls sich P_max auf die pro Sekunde ausführbaren Gleitpunktoperationen bezieht, so erhält man die maximale Gleitpunktleistung mit der Einheit flop/s (floating-point operations per second) bzw. Mflop/s (10⁶ flop/s) oder Gflop/s (10⁹ flop/s).

Tabelle 2 zeigt die maximalen Gleitpunktleistungen der in der Studie verwendeten Computersysteme.

Tabelle 2: Maximale Gleitpunktleistung (eines einzelnen Prozessors)
der verwendeten Computersysteme.

Empirische Gleitpunktleistung: Wenn man die in einem Zeitraum T verrichtete Arbeit durch die Anzahl W_F der in T ausgeführten Gleitpunktoperationen charakterisiert, so erhält man die Gleitpunktleistung (floating-point performance)

.

Im Gegensatz zu der rechnerisch ermittelten Maximalleistung gewinnt man diesen empirischen Wert durch Messungen an laufenden Programmen. Zahlenangaben erfolgen wie bei der analytischen Leistungsbewertung in Mflop/s oder Gflop/s. Für diesen Beitrag wurden nur die Ergebnisse der komplexen FFT-Programme bei Transformationslängen N = 2ⁿ, n  {5, 6, ..., 21} verwendet.

Zeitmessung: Die Tabellen 3 und 4 zeigen gemessene Rechenzeiten von acht verschiedenen FFT-Programmen. In Tabelle 4 sind die Slow-down-Faktoren (relativen Rechenzeiten bezogen auf den jeweils schnellsten Fall) dargestellt. Bemerkenswert ist vor allem das schlechte Abschneiden des NAG-Programms, das durchschnittlich sechsmal mehr Rechenzeit benötigt als die jeweils schnellsten Programme.

Tabelle 3:  Absolute Laufzeiten komplexer FFT-Programme
auf einem Prozessor des ZID-Servers SGI Power Challenge XL.

Tabelle 4: Slow-down-Faktoren (relative Rechenzeiten bezogen auf den
jeweils schnellsten Fall) auf dem ZID-Server SGI Power Challenge XL.

Flop-count: Für eine exakte Bestimmung der empirischen Gleitpunktleistung muss die genaue Anzahl der ausgeführten Gleitpunktoperationen (z. B. mit Hilfe von PMCs¹) bestimmt werden. Wie man aus Abb. 1 erkennen kann, ist die in der Literatur oft verwendete Näherungsformel W_F = 5N log N für die arithmetische Komplexität von FFT-Algorithmen nur sehr ungenau. Würde diese Formel stimmen, dann müsste die normalisierte arithmetische Komplexität W_F /N log N für alle N den konstanten Wert 5 haben. Der Grund für die niedrigeren Werte und für das nichtkonstante Verhalten liegt darin, dass verschiedene FFT-Implementierungen Multiplikationen mit den trivialen Einheitswurzeln 1, -1, i und - i unterschiedlich behandeln (zu vermeiden suchen).

Wirkungsgrad: In Abb. 2 ist die gemessene (empirische) Gleitpunktleistung der fünf leistungsfähigsten FFT-Programme auf dem ZID-Server SGI Cray Origin 2000 in einer Wirkungsgrad-Darstellung zu sehen.

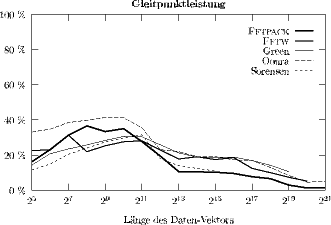
Abbildung 1:  Normalisierter Flop-count (W_F /N log ₂ N) von FFT-Programmen.

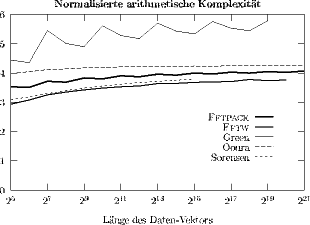
Abbildung 2: Empirische Gleitpunktleistung (Wirkungsgrad) von
FFT-Programmen auf einem Prozessor des ZID-Servers SGI Cray Origin 2000
(100 % entsprechen der theoretischen Maximalleistung von 500 Mflop/s.)

Den Tabellen 5 und 6 können absolute Rechenzeiten und Slow-down-Faktoren (relative Rechenzeiten bezogen auf den jeweils schnellsten Fall) des Programmpakets FFTW entnommen werden. Trotz der unterschiedlichen Maximalleistungen (siehe Tabelle 2) weisen die Workstations (von DEC, IBM und HP) ein relativ ähnliches Leistungsverhalten auf. Die SGI-Server mit ihren relativ niedrigen Maximalleistungen (pro Prozessor) benötigen durchschnittlich 2-3mal so viel Rechenzeit wie die schnellsten Workstations. Bemerkenswert ist das gute Abschneiden des PCs, der bei großen Transformationslängen - wo hohe Leistung besonders wichtig ist - mit den ZID-Servern mithalten kann bzw. die SGI Power Challenge sogar deutlich überholt.

Tabelle 5: Absolute Laufzeiten von FFTW auf verschiedenen Computersystemen.

Tabelle 6: Slow-down-Faktoren (relative Rechenzeiten bezogen auf den
jeweils schnellsten Fall) von FFTW auf verschiedenen Computersystemen.

SGI Cray Origin 2000 vs. SGI Power Challenge XL: In Abb. 3 sind die normalisierten Laufzeiten der fünf leistungsfähigsten FFT-Programme auf der SGI Cray Origin 2000 dargestellt. Die normalisierten Laufzeiten dieser fünf FFT-Programme auf der SGI Power Challenge XL kann man Abb. 4 entnehmen.

Abbildung 3: Normalisierte Laufzeit (T / N log₂ N) von FFT-Programmen auf einem Prozessor des ZID-Servers SGI Cray Origin 2000.

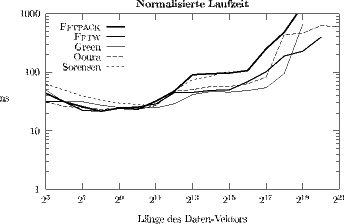
Abbildung 4: Normalisierte Laufzeit (T / N log₂N) von FFT-Programmen
auf einem Prozessor des ZID-Servers SGI Power Challenge XL.

Die MIPS R10000-Prozessoren der SGI Power Challenge werden mit einer Taktfrequenz von 195 MHz betrieben, während die Prozessoren der SGI Cray Origin 2000 mit 250 MHz betrieben werden (Speed-up von 28,2 %).

Solange die FFT-Berechnung lokal im L1-Cache ausgeführt werden kann, spiegelt sich diese Relation auch in den gemessenen Laufzeiten wider. So benötigt z. B. die FFTPACK-Routine für die Transformation eines Vektors der Länge N = 2¹⁰ auf der SGI Power Challenge 0,239 ms; auf der SGI Cray Origin werden 0,187 ms benötigt, was einem Speed-up von 28,3 % entspricht.

Aufgrund des nur 2 MB großen L2-Daten-Caches der SGI Power Challenge weisen dort sämtliche FFT-Routinen deutlich ausgeprägtere Performance-Einbrüche auf als auf der SGI Cray Origin (mit einem L2-Daten-Cache von 4 MB). So hat z. B. die getestete FFTPACK-Routine für Transformationslängen N  2¹⁷, aufgrund von L2-Cache-Misses, einen dramatischen Leistungsabfall auf der SGI Power Challenge XL. Für die Transformation eines Vektors der Länge N = 2¹⁸ benötigt die Power Challenge ungefähr fünfmal so viel Rechenzeit wie die Cray Origin.

Multiply-Add-Optimierte FFT-Programme

Zusätzlich zu den "üblichen" Gleitpunktoperationen, wie Addition, Subtraktion, Multiplikation und Division, besitzen moderne RISC-Prozessoren auch eine Instruktion, die eine Multiplikation und eine davon abhängige Addition - die Operation c (Multiply-Add ) - in derselben Zeit wie eine einzelne Gleitpunkt-Multiplikation oder Addition ausführen kann.

Multiply-Add-Operationen haben einen großen Einfluss auf die Gleitpunktleistung. So hat z.B. der Hochleistungsserver Cray Origin 2000 von SGI eine Zykluszeit von T_c = 4 ns. In einem Taktzyklus können maximal zwei Gleitpunktoperationen - eine Multiply-Add-Instruktion - ausgeführt werden. Als maximale Gleitpunktleistung ergibt sich damit:

.

Je geringer der Anteil der Multiply-Add-Instruktionen an der Gesamtzahl der konkret auszuführenden Gleitpunktoperationen eines Programmes ist, desto weiter entfernt sich die reale Leistung des Rechners von seiner thoretischen Maximalleistung.

In konventionellen FFT-Algorithmen ist die Anzahl der Additionen stets größer als die Anzahl der auszuführenden Multiplikationen. Es ist daher unmöglich, eine Instruktionsanordnung zu finden, die es erlaubt, alle auftretenden Additionen im Rahmen von Multiply-Add-Instruktionen auszuführen. Darüber hinaus ist es nicht einmal möglich, alle Multiplikationen im Rahmen von Multiply-Add-Instruktionen auszuführen. Eine schlechte Ausnutzung der Multiply-Add-Instruktionen (ein schlechter Wirkungsgrad) ist daher bei konventionellen FFT-Implementierungen unvermeidlich. So nutzen z. B. die in diesem Beitrag erwähnten FFT-Routinen die Multiply-Add-Instruktionen nur zu einem Prozentsatz von 20 - 25 % aus.

Den Autoren dieses Beitrags ist es gelungen, zwei völlig neue Klassen von FFT-Algorithmen zu entwickeln, die Multiply-Add-Instruktionen zu 100 % ausnutzen (Karner, Auer, Überhuber [4]):

• Eine Klasse von FFT-Algorithmen mit reduzierter arithmetischer Komplexität, und
• eine Klasse von FFT-Algorithmen, bei der die Anzahl an Speicherzugriffen auf die zur Berechnung benötigten Einheitswurzeln von O(N) auf   reduziert wird.
  

Ausblick

Die Autoren werden ihre Arbeit an der Entwicklung hocheffizienter FFT-Algorithmen und deren Implementierung auf modernen Computersystemen im Rahmen des Spezialforschungsbereiches "AURORA" (SFB 011) unter Förderung durch den FWF fortsetzen. Interessierte Leser sind herzlich eingeladen, mit den Autoren Kontakt aufzunehmen.

Literatur

[1]    M. Auer, F. Franchetti, H. Karner, C. W. Ueberhuber: Performance Evaluation of FFT Algorithms Using Performance Counters. AURORA Tech. Report TR1998-20, Inst. für Angew. und Num. Math., TU Wien, 1998.

[2]    M. Auer, R. Benedik, F. Franchetti, H. Karner, P. Kristöfel, R. Schachinger, A. Slateff, C. W. Ueberhuber: Performance Evaluation of FFT Routines - Machine Independent Serial Programs. AURORA Tech. Report TR1999-05, Inst. für Angew. und Num. Math., TU Wien, 1999.

[3]    J. W. Cooley, J. W. Tukey: An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comp. 19 (1965), pp. 297-301.

[4]    H. Karner, M. Auer, C. W. Ueberhuber: Multiply-Add Optimized FFT Kernels. Math. Models Methods Appl. Sci., erscheint 1999.

[5]    H. J. Nussbaumer: Fast Fourier Transform and Convolution Algorithms. Springer-Verlag, Heidelberg, 1981.

[6]    W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling: Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, Cambridge, 1992.

[7]    C. W. Ueberhuber: Numerical Computation. Springer-Verlag, Heidelberg, 1997.

[8]    C. F. Van Loan: Computational Frameworks for the Fast Fourier Transform. SIAM Press, Philadelphia, 1992.

AURORA-Reports sind über das Internet erhältlich:   http://www.vcpc.univie.ac.at/aurora/publications/